Last week I presented at the Data Science Study Group on a project of mine where I built a deep learning platform from scratch in python.

For reference, here’s my code and slides.

First, my project drew primarily from two sets of sources, without which I never would have completed this project. First, there are many examples of folks doing this online. Here’s an incomplete list in python:

While all of these are useful, Sabinasz’s was what I based my project on because he implements a system that builds a computational graph and includes a true backpropogation algorithm. The others I saw do this implicitly by calculating the gradients operation-by-operation. That approach is fine for a single demo but I wanted something that mimicked the flexibility of tensorflow, allowing me to compare different network structures and activations without starting over each time.

In addition to these resources, I drew heavily from Deep Learning by Goodfellow, Bengio, and Courville. I’m certain that the other examples I looked toward used this book as well.

While I started with Sabinasz’s code, I made a few modifications and improvements including:

  • Add graph visualization with python Graphviz
  • Remove the use of globals for the computational graph
  • Simplify backprop algorithm by adding gradient calculations to the operation classes
  • Add a Relu activation function
  • Tweak the visualizations

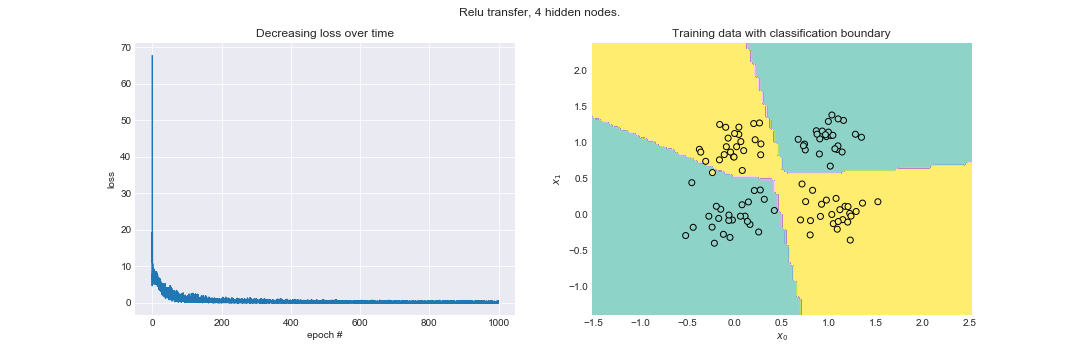
Here’s the learning rate plotted along with the classification boundary for a relu network with 4 hidden nodes.

And here’s the computational graph. You can really see the benefit of tracking the graph and automating the backprop algorithm for a graph of this size.

What I still want to do

  1. I want to write up a blog summarizing my talk and the process for creating this. I think it could be a very useful explanatory tool.
  2. I have a strong feeling that some of the gradients in here are inaccurate.
    • In many cases the network fails to learn for any learning rate schedule unless I give it a much higher capacity than it needs (e.g. 4+ hidden nodes in the XOR task).
    • In simple cases, like separable data, the model should be able to get arbitrarily close to $J=0$ but fails to do so.
    • The softmax gradient seems to differ from that found in other sources
  3. I want to extend this model to larger datasets and deeper networks. Right now it runs into what I think are underflow errors in these cases but they should be possible to avoid.